Stories
I have always enjoyed working with mathematics, just as I have enjoyed learning and using other languages. I could not stand the way it was taught, so both at Columbia when I passed a course in calculus and again at Yale when I passed a course in statistics, I did not go to class, but simply read the books and passed the exams. Later, in working on the linear time model, I would come to the conclusion that it could explain why acceleration, which is the normal motion seen in everyday life, is treated as a special case and uniform motion, which we almost never see, is treated as the normal case.
But when it came time to work as a scientist, I needed to use mathematics and often I would make it up or go to exotic sources to find the tools I needed.
I will present some examples on this page without an elaborate explanation, since they are all taken from articles reprinted in The Aggression Systems on my personal website, where they can be seen and understood in their full context. What the reader should note in the following examples are the quantitative values provided for each relationship. That is the beauty of mathematics, the ability to quantify relationships that would otherwise remain only theoretical. See point 6 in the model for behavioral research that I wrote at the beginning of my scientific career.
Hence, for example in my doctoral dissertation, I needed to be able to say when there were non-random effects on the firing rates of the neurons I was recording. I found out that there is a simple mathematics of random occurrences which is described by the Poisson distribution, so I made up a statistic describing how far a particular firing rate during an experimental procedure differed from its Poisson distribution when the animal was resting quietly. It was simple and elegant. I suppose it has also been used by others, but I have not seen it.
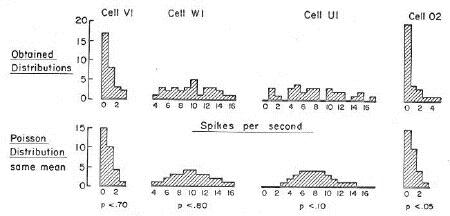
Later, to analyze the behavior sequences of pairs of monkeys and pairs of rats, I found that there was a rather elaborate statistic that could be employed (using large numbers of iterations by a computer) that could tell which sequences of behavior were non-random, and how much so.
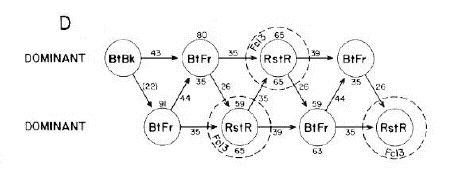
And still later, beginning to apply scientific methods to the questions of war and peace, I was able to use partial correlations to analyze all of the influences on the activity of a student for peace, including the role played by belief systems and the attitudes of those around the person.
Finally, coming back to the challenge of the linear time model, I began work to find a geometry of time.
 |
Stages
1986-1992
Fall of Soviet Empire
1992-1997
UNESCO Culture of Peace Programme